그래프는 지하철 노선도처럼 노드 사이의 연결 관계를 표현할 수 있는 자료구조다.
이에 대해 자세히 알아보자.
그래프의 역사
그래프는 수학자 오일러의 "Konigsberg Bridge Problem - 쾨니히스베르크의 다리 문제"에서 시작했다.
이 문제는 아래 그림과 같이 다리가 연결되어 있는데
임의의 지역에서 모든 다리를 한 번만 건너 출발했던 지역으로 돌아올 수 있는가이다.

오일러는 위 문제를 아래와 같이 간단한 그림으로 표현했으며 토지를 정점, 다리를 간선으로 대체했다.
이것이 그래프(Graph)이다.

https://en.wikipedia.org/wiki/Seven_Bridges_of_K%C3%B6nigsberg
Seven Bridges of Königsberg - Wikipedia
From Wikipedia, the free encyclopedia Classic problem in graph theory Map of Königsberg in Euler's time showing the actual layout of the seven bridges, highlighting the river Pregel and the bridges The Seven Bridges of Königsberg is a historically notabl
en.wikipedia.org
여담으로 이후 그래프에 존재하는 모든 간선을 한 번씩 방문하는 경로를 오일러 경로,
이때 시작 노드와 도착 노드가 같으면 오일러 회로라고 하게 된다.
그래프의 용어
그래프는 정점(vertex)과 간선(edge)으로 이루어져 있다.

이때 정점은 node, 간선은 link로도 불리는데, vertex와 edge가 보편적이다.
차수(degree)는 한 정점에 인접한 정점의 수로 위의 그래프에서 정점 A의 차수는 3이다.
인접 정점(adjacent vertex)은 한 정점에 인접한 정점으로 정점 B의 인접 정점은 정점 A, C이다.
기호로는 그래프 G=(V, E)와 같이 표현한다.(V: 정점, E: 간선)
V(G)는 그래프 G의 정점들의 집합, E(G)는 그래프 G의 간선들의 집합이다.
그래프의 종류
그래프는 다양한 종류가 있다. 이를 차근차근 알아보자.
무방향 그래프 & 방향 그래프
먼저 무방향 그래프(undirected graph)와 방향 그래프(directed graph)이다.

무방향 그래프(G1)는 간선이 화살표가 아닌 선으로, 양방향 이동이 가능하다.
간선은 (A, B)와 같이 나타내며 A에서 B, B에서 A로 이동이 가능함을 의미한다.
V(G1) = {A, B, C, D},
E(G1) = {(A, B), (A, C), (A, D), (B, C)}
방향 그래프(G2)는 간선이 화살표로 이루어져 있고 해당 방향으로만 이동이 가능하다.
간선은 <A, B>와 같이 나타내며 A에서 B로만 이동이 가능함을 의미한다.
만약 B에서 A로도 이동이 가능하다면 <A, B>, <B, A>를 각각 작성해야 한다.
V(G2) = {A, B, C, D},
E(G2) = {<A, D>, <B, A>, <B, C>, <C, A>}
부분 그래프
다음은 부분 그래프(sub graph)이다.
부분 그래프 S는 그래프 G에 대해 V(S) ⊆ V(G), E(S) ⊆ E(G)를 만족한다.
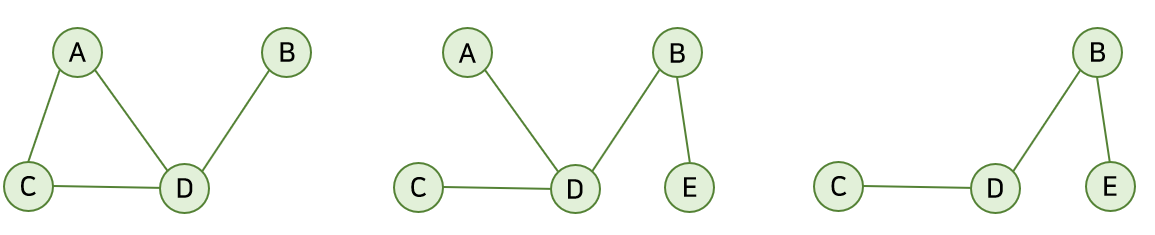
그림으로 보면 이해가 쉬운데, 만약 그래프 G1이 있다고 했을 때

아래 그래프들이 부분 그래프이다. 그래프 G1의 부분으로 이루어져 있는 것을 알 수 있다.
가중치 그래프
가중치 그래프(weighted graph)는 간선에 가중치가 붙은 그래프이다.

네트워크(network)라고도 하며 활용도가 높다.
연결 그래프 & 비연결 그래프
연결 그래프(connected graph)와 비연결 그래프(unconnected graph)는 경로 유무의 차이다.
경로란 '정점 x에서 정점 y까지의 정점의 나열'로 각 정점은 간선으로 이어져 있어야 한다.
아래 그래프를 예로 들었을 때

정점 B에서 정점 E까지의 경로는 B, A, D, E이다. (B, C, A, D, E도 경로이다.)
B, C, E는 정점 C와 정점 E 사이에 간선이 없으므로 경로가 아니다.
(위 경로처럼 반복되는 간선이 없는 경우를 단순 경로(simple path)라고 한다.)
다시 돌아와서 그래프에서 모든 정점에 접근할 수 있는 경로가 있으면 연결 그래프, 아니면 비연결 그래프이다.

위 그림에서 오른쪽 그래프는 정점 D를 갈 수 있는 경로가 없으므로 비연결 그래프이다.
완전 그래프
완전 그래프(complete graph)는 그래프에 속한 모든 정점이 서로 연결된 그래프이다.

무방향 완전 그래프는 정점 수를 n이라고 했을 때 간선 수는 n * (n-1) / 2이다.
그래프의 구현
그래프를 구현하는 방법은
1. 인접 행렬을 이용한 방법 - 2차원 배열 이용
2. 인접 리스트를 이용한 방법 - 연결 리스트 이용
이 있다.
인접 행렬(adjacency matrix) 그래프
먼저 인접 행렬을 이용한 방법을 보자.
아래 그래프에 대한 오른쪽 표가 인접 행렬이다.
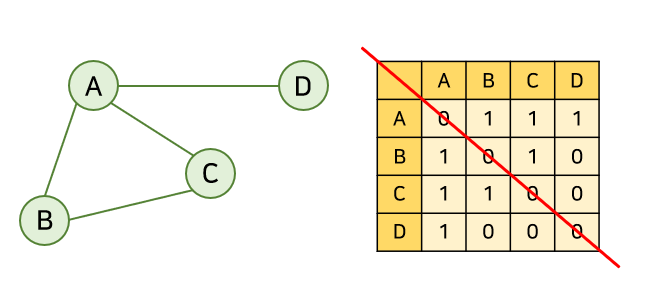
서로 이어져 있는 정점은 1, 이어져 있지 않으면 0으로 표현한다.
위 그래프는 무방향 그래프이기 때문에 중간(빨간 선)을 기준으로 값이 대칭이다.
인접 행렬 그래프는 정점이 n개일 때 n2의 공간이 필요하기 때문에 간선이 많은 그래프에 유리하다.
또, 배열로 구현하기 때문에 간선의 여부를 O(1)로 알 수 있다는 장점이 있다.
구현
인접 행렬 그래프를 구현해 보자.
간단하게 무방향 그래프를 구현하였다.
먼저 Graph 클래스의 인스턴스 변수 선언과 생성자이다.
유지보수를 쉬게 하기 위해 정점의 개수를 받는 VERTEX_NUM을 상수로 선언했고
간선 정보를 담을 이차원 배열 변수 graph를 선언했다.
생성자에선 초기화가 이루어진다.
final int VERTEX_NUM;
int[][] graph;
Graph(int n) {
VERTEX_NUM = n;
graph = new int[VERTEX_NUM][VERTEX_NUM];
}
다음은 동작 메서드이다.
void addVertex(int v1, int v2) {
graph[v1][v2] = 1;
graph[v2][v1] = 1;
}
void print() {
for(int i = 0; i < VERTEX_NUM; i++) {
for(int j = 0; j < VERTEX_NUM; j++)
System.out.print(graph[i][j] + " ");
System.out.println();
}
}addVertex()는 들어오는 값에 따라 인접 행렬 값을 1로 바꾸는 작업을,
print()는 결과를 출력한다.
마지막으로 main() 메서드이다.
public static void main(String[] args) {
Graph g = new Graph(5);
g.addVertex(0, 1);
g.addVertex(0, 2);
g.addVertex(1, 3);
g.addVertex(2, 3);
g.addVertex(3, 4);
g.print();
}Graph 클래스 참조 변수 g를 선언한 후 연결 정점 정보를 담은 후 출력했다.
위 코드의 그래프는 그림으로 보면 아래와 같다. 결과가 올바르게 출력되었음을 알 수 있다.

전체 코드
package practice;
public class Graph_Matrix {
public static void main(String[] args) {
Graph g = new Graph(5);
g.addVertex(0, 1);
g.addVertex(0, 2);
g.addVertex(1, 3);
g.addVertex(2, 3);
g.addVertex(3, 4);
g.print();
}
}
class Graph {
final int VERTEX_NUM;
int[][] graph;
Graph(int n) {
VERTEX_NUM = n;
graph = new int[VERTEX_NUM][VERTEX_NUM];
}
void addVertex(int v1, int v2) {
graph[v1][v2] = 1;
graph[v2][v1] = 1;
}
void print() {
for(int i = 0; i < VERTEX_NUM; i++) {
for(int j = 0; j < VERTEX_NUM; j++)
System.out.print(graph[i][j] + " ");
System.out.println();
}
}
}
인접 리스트(adjacency list) 그래프
다음은 연결 리스트를 이용하는 인접 리스트 그래프이다.
아래 그림이 인접 리스트 그래프의 동작 모습이다.
각 정점마다 인접 정점의 정보를 리스트로 담고 있음을 알 수 있다.
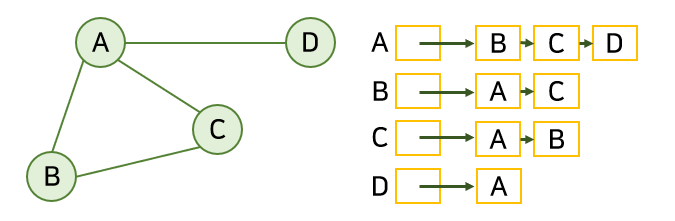
위 그래프는 무방향 그래프이기 때문에 A 리스트에 B가, B리스트에 A가 있다.
만약 <A, B>라면 리스트 B에는 A가 없다.
인접 리스트 그래프는
무방향 그래프의 경우 정점이 n개면 n개의 연결 리스트가, 간선이 e개라면 2e개의 리스트 노드가 필요하다.
따라서 간선의 수가 적은 그래프에 유리하다.
연결 리스트로 구현하기 때문에 전체 간선의 수를 알기 위한 시간복잡도는 O(n + e)이다.
구현
인접 리스트 그래프도 간단하게 무방향 그래프로 구현해 보았다.
먼저 인스턴스 변수와 생성자이다.
변수 선언과 초기화가 이루어진다.
final int VERTEX_NUM;
ArrayList <ArrayList<Integer>> list = new ArrayList<>();
Lgraph(int n) {
VERTEX_NUM = n;
for(int i = 0; i < VERTEX_NUM; i++)
list.add(new ArrayList<>());
}
다음은 메서드이다.
void addVertex(int v1, int v2) {
list.get(v1).add(v2);
list.get(v2).add(v1);
}
void print() {
for(int i = 0; i < VERTEX_NUM; i++) {
System.out.println(i + ": " + list.get(i).toString());
}
}무방향 그래프이므로 addVertex에서 각각에 대해 add를 해준다.
마지막으로 main() 메서드이다.
public static void main(String[] args) {
Lgraph g = new Lgraph(5);
g.addVertex(0, 1);
g.addVertex(0, 2);
g.addVertex(1, 3);
g.addVertex(2, 3);
g.addVertex(3, 4);
g.print();
}인접 배열 그래프와 동일하게 동작한다.
아래는 결과이다. 값이 올바르게 담긴 것을 확인할 수 있다.
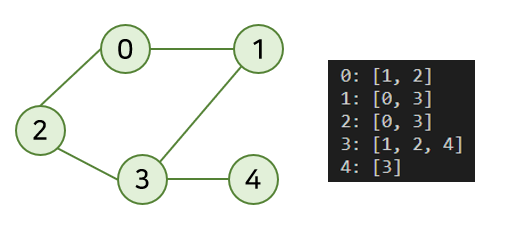
전체 코드
package practice;
import java.util.ArrayList;
public class Graph_List {
public static void main(String[] args) {
Lgraph g = new Lgraph(5);
g.addVertex(0, 1);
g.addVertex(0, 2);
g.addVertex(1, 3);
g.addVertex(2, 3);
g.addVertex(3, 4);
g.print();
}
}
class Lgraph {
final int VERTEX_NUM;
ArrayList <ArrayList<Integer>> list = new ArrayList<>();
Lgraph(int n) {
VERTEX_NUM = n;
for(int i = 0; i < VERTEX_NUM; i++)
list.add(new ArrayList<>());
}
void addVertex(int v1, int v2) {
list.get(v1).add(v2);
list.get(v2).add(v1);
}
void print() {
for(int i = 0; i < VERTEX_NUM; i++) {
System.out.println(i + ": " + list.get(i).toString());
}
}
}'Data Structure' 카테고리의 다른 글
| 자료구조 - Stack, Queue, Deque (1) | 2023.08.27 |
|---|---|
| 자료구조 - 전위, 중위, 후위 표기법 (0) | 2023.08.24 |
| 자료구조 - 이진 트리(전위, 중위, 후위, 레벨 순회) (0) | 2023.08.24 |