출발지에서 목적지까지 가는 방법이 여러 가지인 것처럼
어떤 문제를 풀 때 하나의 알고리듬만 있는 것이 아니다.
x * y만 해도 Long Multiplication, Lattice Multiplication, Peasant Multiplication 등 방법이 다양하다.
그렇다면 다양한 알고리듬 중 어떤 것이 더 좋은지 어떻게 구분할까?
시간복잡도 & 공간복잡도를 알아보자.
공간복잡도(Space Complexity)
공간복잡도는(Space Complexity)는 알고리듬 실행에 필요한 저장 공간을 나타낸다.
만약 알고리즘 1이 10MB, 알고리즘 2가 100MB만큼의 저장 공간을 요구한다면
공간 복잡도 측면에서 알고리즘 1이 알고리즘 2보다 효율적인 것이다.
하지만 알고리듬의 복잡도를 따질 때 공간복잡도는 시간복잡도에 비해 사용 빈도가 낮은데, 그 이유는
1. 대부분의 프로그램 환경에서 공간에 대한 비용보다 시간에 대한 비용이 더 크기 때문
2. 메모리는 쉬운 재사용, 확장이 가능한 반면 실행에 필요한 시간은 쉽게 단축할 수 없기 때문
등이 있다.
즉, 메모리는 물리적으로 보충이 가능하지만 시간은 그럴 수 없기 때문이다.
시간복잡도(Time Complexity)
시간복잡도(Time Complexity)는 알고리듬의 수행 시간을 이론적으로 분석하기 위한 개념이다.
시간복잡도 측정은
1. 알고리즘을 실행하여 직접 시간을 측정하는 경우
2. 실행되는 알고리즘의 연산 개수를 계산하는 경우
두 가지 방법이 있는데, 직접 시간을 측정하는 경우는 외부 요인(구현 언어, HW 스펙 등)에 의한 차이가 있으므로
외부 요인을 따지지 않는 2번 방법을 사용해 시간복잡도를 측정한다.
코드에서 각 연산마다 걸리는 시간은 거의 동일하므로 시간복잡도는 실행되는 연산의 개수(n)를 센다.
하지만, if문, for문 등 상황마다 연산의 개수가 달라질 수 있으므로 수치를 근사화(단순화)하여 분석한다.
시간복잡도를 구하는 유형은 아래 3가지이다.
- Best-case Analysis : 가장 적은 시간
- 연산 개수가 가장 적을 때를 구한다. 하지만 구한다고 해도 의미가 없는 값이다. - Worst-case Analysis : 가장 오랜 시간
- 연산 개수가 가장 많을 때를 구한다. 수행시간의 상한을 구하는 것이기 때문에 의미가 있고 주로 사용한다. - Average-case Analysis : 평균 시간
- 연산의 평균을 구한다. 경우의 수가 많아 구하기 어렵다.
Big - O Notation
시간복잡도를 표현할 땐 Big-O 표기법을 이용한다.
Big-O 표기법은 두 함수간 관계를 나타내는 표기법으로 함수의 증가 속도를 비교한다.
이때, 증가 속도는 n이 무한대로 갈 때 어떤 함수가 더 빠르게 증가하는가를 의미한다.
이외에도 Big-Ω(오메가), Big-Θ(세타)가 있다.
이 표기법들은 시간복잡도와 별개로 원래 존재했다. 즉, 시간복잡도 때문에 나온 표기법이 아니다.
3가지 표기법
Big-O와 유사하게 Big-Ω(빅-오메가)와 Big-Θ(빅-세타)가 있다.
1. Big-O : f(n) = O(g(n))일 때, f의 증가속도는 g보다 빠르지 않다. (비슷하거나 느리다.)
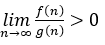
를 만족해야 한다. 즉, 무한으로 발산하거나 양수로 수렴해야 한다.
2. Big-Ω : f(n) = Ω(g(n))일 때, f의 증가속도는 g보다 느리지 않다. (비슷하거나 빠르다.)

를 만족해야 한다. 즉, 무한으로 발산하거나 양수로 수렴해야 한다.
3. Big-Θ : f(n) = Θ(g(n))일 때, f의 증가속도는 g와 비슷하다.
f(n) = O(g(n))이고 f(n) = Ω(g(n))일 때

가 발산하지 않고 0이 아닌 양수로 수렴해야 한다.
Big - O 표기법을 사용하는 이유는 아래와 같다.
- 시간복잡도를 계산할 때 가장 중요한 것은 최악의 경우이다.
- 알고리즘의 최악의 경우를 정확히 계산하기 어렵고 복잡하다. 따라서 대략적으로 표기할 방법이 필요하다.
- 추상적인 대상으로서 상수가 덜 중요하다.
수행시간이 적은 알고리즘

위 그래프는 Big-O 함수들을 비교한 것으로 완만할수록 좋다.
즉, O(n)이 O(1) 보다 느리고 O(n long n) 보다 빠른 것이다.
시간복잡도 예시
시간복잡도를 보이기 위해 1 ~ N까지 더하는 알고리듬을 만들어보자.
1. for문을 이용해 더하는 방법
쉽게 떠오르는 방법으로 1~N까지 차례대로 더한다.
이때, N의 값이 1 증가하면 따라 for문 실행 횟수도 1 증가하므로 시간복잡도는 O(N)이다.
for (i = 1; i <= n; i++) {
sum = sum + i;
}
2. 등차수열의 합을 이용하는 방법
1~N까지 더하는 것이므로 등차수열의 합 공식(n(1+n)/2)을 이용해 풀 수 있다.
이 방법은 n에 값을 대입하면 되므로 for문을 사용하지 않는다.
N의 값이 무엇이든 연산을 한 번만 하므로 시간복잡도는 O(1)이다. N에 관련이 없다는 의미이다.
즉 2번 알고리듬이 1번 알고리듬에 비해 좋다고 말할 수 있다.
'Algorithm & PS > Algorithm' 카테고리의 다른 글
| 알고리듬 - 버블, 선택, 삽입 정렬 (0) | 2023.06.27 |
|---|---|
| 알고리듬 - 슬라이딩 윈도우 (0) | 2023.06.26 |
| 알고리듬 - 투 포인터 (0) | 2023.06.26 |
| 알고리듬 - 구간 합 (0) | 2023.06.24 |
| 알고리듬 - dx, dy를 이용한 이차원 배열 이동 (0) | 2023.06.21 |