알고리듬 - 깊이 우선 탐색, 너비 우선 탐색
깊이 우선 탐색(DFS: Depth-First Search)과 너비 우선 탐색(BFS:Breadth-First Search)은
그래프 완전 탐색 기법 중 하나이다. 이 둘에 대해 알아보자.
깊이 우선 탐색(DFS)
DFS는 그래프의 시작 노드에서 출발해 한쪽 분기를 최대 깊이까지 탐색한 후 다른 쪽 분기를 탐색하는 형식이다.
방문한 정점을 시작 정점으로 하여 다시 탐색을 진행하는 방식으로 진행한다.
DFS는 노드 수를 V, 간선 수를 E라고 했을 때
그래프가 인접 리스트로 구현되었으면 시간복잡도가 O(V + E),
그래프가 인접 행렬으로 구현되었으면 시간복잡도가 O(n2)이다.
동작 그림으로 보자.
아래와 같은 그래프가 있고 정점 0을 시작 정점으로 하였다.

정점 1을 먼저 탐색한다고 했을 때, 다시 정점 1이 시작 정점이 되어 다른 정점을 탐색한다.

서로 이어져 있는 정점 2, 3, 4도 같은 방식으로 진행한다.

정점 4에선 더 이상 탐색할 곳이 없으므로 되돌아간다.

정점 3으로 돌아간 후에도 더 이상 탐색할 곳이 없으므로 되돌아간다.

정점 2, 1, 0에서도 탐색할 곳이 없으므로 모든 노드를 탐색한 것이고 DFS는 종료된다.
만약 아래와 같이 정점 1, 정점 2가 연결되어 있지 않다면

정점 1을 먼저 간다고 했을 때, 정점 1에선 더 이상 탐색할 곳이 없으므로 정점 0으로 돌아간 후 정점 2로 간다.

구현
그럼 DFS를 간단하게 구현해 보자.
DFS는 재귀함수 혹은 Stack을 이용해 구현할 수 있다.
먼저 Stack을 활용한 DFS이다.
int NODE_NUM = 5;
int[][] graph = {
{0, 1, 1, 0, 0},
{1, 0, 0, 0, 0},
{1, 0, 0, 1, 1},
{0, 0, 1, 0, 1},
{0, 0, 1, 1, 0}
};그래프의 모양인데 그림으로 보면 아래와 같다.

아래는 DFS 동작 코드이다.
void dfs(int node) {
//노드를 방문했는지 확인을 위한 boolean 배열
boolean[] visited = new boolean[NODE_NUM];
//DFS 동작을 위한 Stack
Stack<Integer> stack = new Stack<>();
stack.push(node);
while(!stack.isEmpty()) {
int n = stack.pop();
visited[n] = true;
for(int i = 0 ; i < NODE_NUM; i++) {
//만약 node와 이어져있고 방문을 하지 않았다면
if(!visited[i] && graph[n][i] == 1) {
//해당 노드를 stack에 담고 true로 변경
stack.push(i);
visited[i] = true;
}
}
//결과 출력
System.out.println(stack.toString());
}
}정점 0부터 이어진 정점을 Stack에 담기 시작한다.

출력 결과는 위와 같은데, 정점 0과 이어진 1, 2가 먼저 담기고
2와 이어진 3, 4 가 다음에 담긴 것을 확인할 수 있다.
전체 코드
package practice;
import java.util.*;
public class DFS_Stack {
int NODE_NUM = 5;
int[][] graph = {
{0, 1, 1, 0, 0},
{1, 0, 0, 0, 0},
{1, 0, 0, 1, 1},
{0, 0, 1, 0, 1},
{0, 0, 1, 1, 0}
};
DFS_Stack() {
dfs(0);
}
void dfs(int node) {
//노드를 방문했는지 확인을 위한 boolean 배열
boolean[] visited = new boolean[NODE_NUM];
//DFS 동작을 위한 Stack
Stack<Integer> stack = new Stack<>();
stack.push(node);
while(!stack.isEmpty()) {
int n = stack.pop();
visited[n] = true;
for(int i = 0 ; i < NODE_NUM; i++) {
//만약 node와 이어져있고 방문을 하지 않았다면
if(!visited[i] && graph[n][i] == 1) {
//해당 노드를 stack에 담고 true로 변경
stack.push(i);
visited[i] = true;
}
}
//결과 출력
System.out.println(stack.toString());
}
}
public static void main(String[] args) {
new DFS_Stack();
}
}
다음은 재귀를 이용한 구현이다.
재귀는 이전과 다른 그래프를 이용해 보았다.
int[][] graph = {
{0, 0, 1, 0, 0},
{0, 0, 0, 1, 0},
{1, 0, 0, 1, 1},
{0, 1, 1, 0, 1},
{0, 0, 1, 1, 0}
};이런 모양이다.

다음은 재귀 코드이다.
void dfsRecursion(int node) {
//현재 노드를 방문했음으로 바꾼다.
visited[node] = true;
//출력
System.out.println("현재 노드: " + node);
//현재 노드와 연결되어 있고 방문하지 않은 노드를 찾아 재귀
for(int i = 0; i < NODE_NUM; i++)
if(!visited[i] && graph[node][i] == 1)
dfsRecursion(i);
}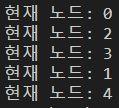
올바른 순서로 방문한 것을 알 수 있다.
전체 코드
package practice;
public class DFS_Recursion {
int NODE_NUM = 5;
boolean[] visited = new boolean[NODE_NUM];
int[][] graph = {
{0, 0, 1, 0, 0},
{0, 0, 0, 1, 0},
{1, 0, 0, 1, 1},
{0, 1, 1, 0, 1},
{0, 0, 1, 1, 0}
};
DFS_Recursion() {
dfsRecursion(0);
}
void dfsRecursion(int node) {
//현재 노드를 방문했음으로 바꾼다.
visited[node] = true;
//출력
System.out.println("현재 노드: " + node);
//현재 노드와 연결되어 있고 방문하지 않은 노드를 찾아 재귀
for(int i = 0; i < NODE_NUM; i++)
if(!visited[i] && graph[node][i] == 1)
dfsRecursion(i);
}
public static void main(String[] args) {
new DFS_Recursion();
}
}
너비 우선 탐색(BFS)
BFS는 시작 정점으로부터 가장 가까운 정점을 순서대로 방문하는 방법으로 Queue를 이용한다.
해당 알고리듬은 시작 노드에서 목표 노드에 도착하는 경로가 여러 개일 때 최단 경로를 보장한다.
BFS는 노드 수를 V, 간선 수를 E라고 했을 때
그래프가 인접 리스트로 구현되었으면 시간복잡도가 O(V + E),
그래프가 인접 행렬으로 구현되었으면 시간복잡도가 O(n2)이다.
동작 그림을 보자.
아래와 같은 그래프를 예로 들었을 때

정점 0과 인접한 노드들을 Queue에 담는다. 현재 연결되어 있는 1, 2, 4가 담긴 모습이다.

다음으로 Queue에서 값을 하나씩 빼면서 해당 노드를 방문한다.

정점 2를 방문했을 때, 연결되어 있는 정점 3이 Queue에도 없고 방문한 적도 없으므로 새롭게 enqueue 한다.

이후 Queue에 값이 없으면 종료한다.
동작 결과 0 - 1 - 2 - 4 - 3 순으로 접근했음을 알 수 있는데 시작 정점 0에서부터 점점 멀어지는 모습이다.
구현
간단하게 BFS를 구현해 보자.
먼저 그래프는 아래와 같다.
int NODE_NUM = 5;
boolean[] visited = new boolean[NODE_NUM];
int[][] graph = {
{0, 1, 1, 0, 0},
{1, 0, 0, 0, 0},
{1, 0, 0, 1, 1},
{0, 0, 1, 0, 1},
{0, 0, 1, 1, 0}
};그림으로 보면 이런 모습이다.

다음은 BFS 코드이다.
public void bfs() {
//노드 순서를 위한 Queue
Queue<Integer> queue = new LinkedList<>();
//시작 노드 0
int start = 0;
queue.offer(start);
visited[start] = true;
//Queue가 빌 때까지
while(!queue.isEmpty()) {
//Queue에서 하나 뺀 후
int node = queue.poll();
//해당 노드와 인접해 있고 방문하지 않은 노드를 Queue에 담는다.
for(int i = 0; i < NODE_NUM; i++) {
if(!visited[i] && graph[node][i] == 1) {
queue.offer(i);
visited[i] = true;
}
}
//출력
System.out.println(queue.toString());
}
}
전체 코드
package practice;
import java.util.LinkedList;
import java.util.Queue;
public class BFS {
int NODE_NUM = 5;
boolean[] visited = new boolean[NODE_NUM];
int[][] graph = {
{0, 1, 1, 0, 0},
{1, 0, 0, 0, 0},
{1, 0, 0, 1, 1},
{0, 0, 1, 0, 1},
{0, 0, 1, 1, 0}
};
BFS() {
bfs();
}
public void bfs() {
//노드 순서를 위한 Queue
Queue<Integer> queue = new LinkedList<>();
//시작 노드 0
int start = 0;
queue.offer(start);
visited[start] = true;
//Queue가 빌 때까지
while(!queue.isEmpty()) {
//Queue에서 하나 뺀 후
int node = queue.poll();
//해당 노드와 인접해 있고 방문하지 않은 노드를 Queue에 담는다.
for(int i = 0; i < NODE_NUM; i++) {
if(!visited[i] && graph[node][i] == 1) {
queue.offer(i);
visited[i] = true;
}
}
//출력
System.out.println(queue.toString());
}
}
public static void main(String[] args) {
new BFS();
}
}