자료구조 - Stack, Queue, Deque
Stack과 Queue는 여러 알고리듬에 사용되는 간단하면서도 중요한 자료구조이다.
이 둘에 대해 알아보자.
Stack
Stack은 후입선출(LIFO: Last In First Out) 형태의 자료구조로 데이터 삽입과 삭제가 한쪽에서만 일어난다.
간단하게 용어를 살펴보면 아래와 같다.

실생활의 경우를 예로 들면 웹페이지 뒤로 가기 기능, 쌓아놓은 상자 등이 있다.
메서드를 호출할 때에도 스택이 활용되는데, 아래 코드를 보자.
public static void main(String[] args) {
System.out.println("main 메서드 시작");
method_1();
System.out.println("main 메서드 종료");
}
static void method_1() {
System.out.println("method_1 메서드 시작");
method_2();
System.out.println("method_1 메서드 종료");
}
static void method_2() {
System.out.println("method_2 메서드 시작");
method_3();
System.out.println("method_2 메서드 종료");
}
static void method_3() {
System.out.println("method_3 메서드 시작");
System.out.println("method_3 메서드 종료");
}main() 메서드가 method_1()을 호출,
method_1() 메서드가 method_2()를 호출,
method_2() 메서드가 method_3()을 호출한다.
아래는 결과이다.

마지막으로 호출한 method_3()이 먼저 끝나고 main()이 가장 나중에 끝난 것을 볼 수 있다.
이는 아래와 같이 쌓인 것인데, 호출받은 메서드가 호출한 메서드 위에 적재된다.

이후 작업이 끝나면 삭제된다.

구현
그럼 간단하게 구현해 보자.
Stack을 구현하는데 기본적으로 필요한 것은 push(), pop(), peek(), isEmpty(), isFull()이다.
각각의 역할은 다음과 같다.
push(): stack에 값을 삽입한다.
peek(): stack 맨 위 값을 반환한다.(삭제 X)
pop(): stack 맨 위 값을 반환하고 삭제한다.
isEmpty(): stack이 비어있는지 확인한다.
isFull(): stack이 꽉 찼는지 확인한다.
사실 List를 활용하면 isFull()는 없어도 되지만
배열을 활용할 것이기 때문에 필요하다.
먼저 사용하는 변수는 아래와 같다.
final int STACK_SIZE = 5;
int top = -1;
int[] stack = new int[STACK_SIZE];스택 값 변경이 쉽게 STACK_SIZE를 상수로 하고 값에 맞게 int형 배열을 선언했다.
top은 요소의 개수를 담을 변수로 처음엔 아무것도 담겨있지 않아 -1로 초기화했다.
isEmpty() & isFull() 메서드
boolean isEmpty() {
return top == -1;
}
boolean isFull() {
return top == STACK_SIZE -1;
}top을 이용해 각각에 대해 true / false를 반환한다.
push() 메서드
void push(int n) {
if(!isFull()) {
stack[++top] = n;
System.out.println("push: " + n + "을 추가했습니다.");
} else
System.out.println("Stack이 꽉 찼습니다.");
}만약 stack이 꽉 차있으면 더 이상 값을 담을 수 없으므로 if문으로 확인한다.
pop() & peek() 메서드
int pop() {
if(!isEmpty()) {
return stack[top--];
} else
System.out.println("Stack이 비어있습니다.");
return -1;
}
int peek() {
if(!isEmpty())
return stack[top];
else
System.out.println("Stack이 비어있습니다.");
return -1;
}pop()과 peek() 두 메서드는 top 부분을 제외하고는 동일하다.
추가로 결과를 출력하기 위한 print() 메서드를 만들었다.
void print() {
System.out.print("Stack: ");
for(int i = 0; i <= top; i++)
System.out.print(stack[i] + " ");
System.out.println();
}
위 코드를 바탕으로 실행해보았다.
s.push(1);
s.push(2);
s.push(3);
s.print();
s.push(4);
s.push(5);
s.push(6);
s.print();먼저 1~3, 4~6을 때 print()를 호출했다. 결과는 아래와 같다.

Stack의 최대 크기가 5이므로 6은 스택에 담기지 못한 모습이다.

다음은 pop()과 peek()를 활용해 보았다.
System.out.println("pop: " + s.pop() + "을 꺼냈습니다.");
System.out.println("pop: " + s.pop() + "을 꺼냈습니다.");
System.out.println("pop: " + s.pop() + "을 꺼냈습니다.");
System.out.println("peek: " + s.peek() + "을 확인했습니다.");
s.print();pop()을 3번 한 후 peek()를 1번 호출했다.

맨 위에 있던 5부터 시작해 4, 3을 꺼냈다.
2는 peek()를 호출한 것이므로 stack에서 삭제되지 않았다.

전체 코드
package practice;
public class StackMain {
final int STACK_SIZE = 5;
int top = -1;
int[] stack = new int[STACK_SIZE];
public static void main(String[] args) {
StackMain s = new StackMain();
s.push(1);
s.push(2);
s.push(3);
s.print();
s.push(4);
s.push(5);
s.push(6);
s.print();
System.out.println("pop: " + s.pop() + "을 꺼냈습니다.");
System.out.println("pop: " + s.pop() + "을 꺼냈습니다.");
System.out.println("pop: " + s.pop() + "을 꺼냈습니다.");
System.out.println("peek: " + s.peek() + "을 확인했습니다.");
s.print();
}
boolean isEmpty() {
return top == -1;
}
boolean isFull() {
return top == STACK_SIZE - 1;
}
void push(int n) {
if(!isFull()) {
stack[++top] = n;
System.out.println("push: " + n + "을 추가했습니다.");
} else
System.out.println("Stack이 꽉 찼습니다.");
}
int pop() {
if(!isEmpty()) {
return stack[top--];
} else
System.out.println("Stack이 비어있습니다.");
return -1;
}
int peek() {
if(!isEmpty())
return stack[top];
else
System.out.println("Stack이 비어있습니다.");
return -1;
}
void print() {
System.out.print("Stack: ");
for(int i = 0; i <= top; i++)
System.out.print(stack[i] + " ");
System.out.println();
}
}
Stack은 깊이 우선 탐색(DFS), 백트래킹 외에도 여러 부분에 사용되므로 매우 중요하다.
Queue
Queue는 선입선출(FIFO: First In First out) 형태로 데이터 삽입과 삭제가 양방향에서 일어난다.
간단하게 용어를 살펴보면 아래와 같다.
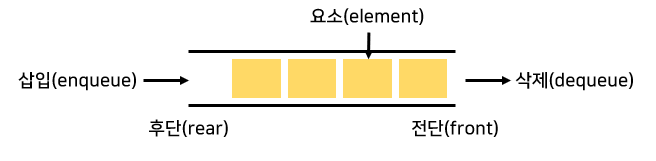
위와 같이 한쪽에서 삽입, 반대쪽에서 삭제가 이루어지는 일자 형으로 되어있는 큐를
선형 큐(Linear Queue)라고 한다.
위 큐를 배열로 구현한다고 가정했을 때 동작을 자세히 보자.
큐의 첫 번째 요소를 가리키는 front, 큐의 마지막 요소를 가리키는 rear 변수는 다음과 같이 동작한다.

이때 요소가 poll 되면

이런 식으로 front가 앞으로 움직이는데, 이때 선형 큐의 문제점이 나타난다.
- front와 rear의 값이 계속 증가하기만 하기에 언젠간 배열의 끝에 도달한다.
- 배열의 앞부분이 비어 있어도 사용할 수 없다.
이를 보완하기 위해 등장한 다른 형태의 큐가 있는데 바로 원형 큐(Circular Queue)이다.
원형 큐는 front 혹은 rear의 값이 배열의 끝에 도달하면 다시 0이 된다.
그림으로 살펴보면 다음과 같다.

이 동작은 선형보다 원형으로 보면 이해가 더 쉽다.

이처럼 동작하는 것이다.
이외에도 덱(Deque)이 있는데 이는 큐의 전단과 후단 모두에서 삽입, 삭제가 가능한 자료구조이다.

구현
이번엔 원형 큐를 구현해 보자.
원형 큐에서 필수적인 메서드는 isEmpty(), isFull(), enqueue(), dequeue(), peek()이다.
역할은 다음과 같다.
enqueue(): queue에 값을 삽입한다.
dequeue(): queue 맨 앞 값을 반환하고 삭제한다.
peek(): queue 맨 앞 값을 반환한다.(삭제 X)
isEmpty(): queue가 비어있는지 확인한다.
isFull(): queue가 꽉 찼는지 확인한다.
사용하는 변수는 다음과 같다.
final int QUEUE_SIZE = 5;
int front = 0, rear = 0;
int eNum = 0;
int[] queue = new int[QUEUE_SIZE];Stack때와 같이 QUEUE_SIZE를 상수로 정한 후 배열을 선언했다.
front와 rear은 요소에 따라 변하는 변수이고 eNum은 요소의 개수를 저장하는 변수이다.
isEmpty() & isFull() 메서드
boolean isEmpty() {
return eNum == 0;
}
boolean isFull() {
return eNum == QUEUE_SIZE;
}eNum의 값에 따라 true/false를 반환한다.
enqueue() 메서드
void enqueue(int n) {
if(!isFull()) {
queue[rear] = n;
rear = (rear + 1) % QUEUE_SIZE;
eNum++;
System.out.println("enqueue: " + n + "을 추가했습니다.");
} else
System.out.println("Queue가 꽉 찼습니다.");
}원형 큐를 구현한 것이기 때문에 rear의 값이 QUEUE_SIZE를 넘지 않도록 나머지 연산자를 활용했다.
dequeue()) & peek() 메서드
int dequeue() {
if(!isEmpty()) {
front = (front + 1) % QUEUE_SIZE;
eNum--;
return queue[front - 1];
}
System.out.println("Queue가 비어있습니다.");
return -1;
}
int peek() {
if(!isEmpty())
return queue[front];
System.out.println("Queue가 비어있습니다.");
return -1;
}dequeue도 나머지 연산자를 활용했다.
print() 메서드
void print() {
for(int i = 0; i < eNum; i++) {
System.out.print(queue[(front + i) % QUEUE_SIZE] + " ");
}
System.out.println();
}마지막으로 출력을 위한 print() 메서드이다.
다음은 실행 내용이다.
q.enqueue(1);
q.enqueue(2);
q.enqueue(3);
q.print();
q.enqueue(4);
q.enqueue(5);
q.enqueue(6);
q.print();먼저 3까지 넣었을 때와 6까지 넣었을 때 print()를 호출했다.
결과는 아래와 같다. Queue가 꽉 차서 6은 담기지 않았다.

다음으로 dequeue를 했을 때이다.
System.out.println("dequeue: " + q.dequeue() + "을 꺼냈습니다.");
System.out.println("dequeue: " + q.dequeue() + "을 꺼냈습니다.");
System.out.println("dequeue: " + q.dequeue() + "을 꺼냈습니다.");
System.out.println("peek: " + q.peek() + "을 확인했습니다.");
q.print();3번 deueue() 후 peek()를 호출했다.
결과는 아래와 같다.

1 - 2 - 3 - 4 - 5 순서로 담았기 때문에 나오는 것도 1부터이다.
따라서 1, 2, 3이 Queue에서 나왔고 4, 5가 남은 모습이다.
전체코드
package practice;
public class QueueMain {
final int QUEUE_SIZE = 5;
int front = 0, rear = 0;
int eNum = 0;
int[] queue = new int[QUEUE_SIZE];
public static void main(String[] args) {
QueueMain q = new QueueMain();
q.enqueue(1);
q.enqueue(2);
q.enqueue(3);
q.print();
q.enqueue(4);
q.enqueue(5);
q.enqueue(6);
q.print();
System.out.println("dequeue: " + q.dequeue() + "을 꺼냈습니다.");
System.out.println("dequeue: " + q.dequeue() + "을 꺼냈습니다.");
System.out.println("dequeue: " + q.dequeue() + "을 꺼냈습니다.");
System.out.println("peek: " + q.peek() + "을 확인했습니다.");
q.print();
}
boolean isEmpty() {
return eNum == 0;
}
boolean isFull() {
return eNum == QUEUE_SIZE;
}
void enqueue(int n) {
if(!isFull()) {
queue[rear] = n;
rear = (rear + 1) % QUEUE_SIZE;
eNum++;
System.out.println("enqueue: " + n + "을 추가했습니다.");
} else
System.out.println("Queue가 꽉 찼습니다.");
}
int dequeue() {
if(!isEmpty()) {
front = (front + 1) % QUEUE_SIZE;
eNum--;
return queue[front - 1];
}
System.out.println("Queue가 비어있습니다.");
return -1;
}
int peek() {
if(!isEmpty())
return queue[front];
System.out.println("Queue가 비어있습니다.");
return -1;
}
void print() {
for(int i = 0; i < eNum; i++) {
System.out.print(queue[(front + i) % QUEUE_SIZE] + " ");
}
System.out.println();
}
}
Queue는 너비 우선 탐색(BFS) 등 여러 부분에 사용된다.